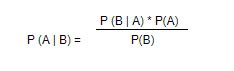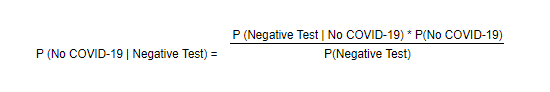A recent announcement from Abbott introduces a cheap ($5) and fast (15 minutes) COVID-19 antigen test. This test is a vast improvement over the current tests that require days and sometimes weeks to return results. With current production ramping up to 50 million tests a month, this new test will help lead to a return to normalcy in the United States.
From the above announcment, a clinical study concluded that the test demonstrates sensitivity of 97.1% and specificity of 98.5%. In this post, I am going to explain what exactly sensitivity and specificity mean, and how this example can explain the Baye’s Theorem.
Baye’s Theorem
To explain specificity and sensitivity, I can make the following statement : From the COVID-19 test above, if a patient receives a positive test, then that patient has a 97.1% probability of actually being positive. Similarily, if the patient receives a negative test, then that patient has a 98.5% chance of actually being negative.
Baye’s Theorem goes a step further by incorporting our prior knowledge about COVID-19 prevalence in the United States. Currently, approximately 1% of the United States population is infected with COVID-19 (estimated from link). Using Baye’s Theorem, we can use this knowledge to calculate what the probability of actually having COVID-19 is given a patient receives a positive test.
The Baye’s Theorem formula is below :
Where,
- P(A) is the probability of event A.
- P(B) is the probability of event B.
- P(A/B) is the probability of observing event A if B is true.
- P(B/A) is the probability of observing event B if A is true.
To illustrate this using the COVID-19 example, I can write the Baye’s Theorem formula as :
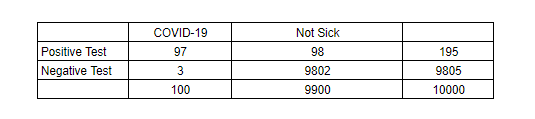
I will use the following table to illustrate the testing outcome of a hypothetical population of 10,000 patients :
Using this scenario and the above table, I compute the following :
- P(COVID-19) is the unconditional probability of having COVID-19 = 100/10,000 = 1%.
- P(Positive Test) is the unconditional probability of a positive test = 195/10,000 = 1.95%.
- P(Positive Test / COVID-19) is the sensitivity of the test = 97/100 = 97% (rounded in this example).
To compute our statistic of interest, P(COVID-19/Positive Test), I can use the formula to calculate (.971) * (.01) / (.0195) = 49.8%. What exactly does this mean? This means that contrary to the intuitive belief that 97.1% of people who test positive actually have COVID-19, in reality, 49.8% of people who test positive actually have COVID-19. This is illustrated in the positive test row in the hypothetical population table above.
Similarly, I can compute the P(No COVID-19/Negative Test) as :
From the table, the calculation is (.985) * (.99) / (.9805) = 99.45%. This is close to the specificity of the test and is not a suprising result given the estimate that 99% of the population does not have COVID-19.
Conclusion
The new COVID-19 test from Abbott offers promise for helping the United States remove to normalcy. Decision makers and public health experts need to understand the above calculations concerning Baye’s Theorem when evaluating new tests and what it means for policy. From above, it is important to realize that patients receiving a negative test can be confident that they don’t actually have COVID-19. However, patients receiving a positive test only have about a 50% chance of having COVID-19. This is important as it ensures that there is a limited amount of people who are testing negative and not isolating when in fact they have COVID-19. This errs on the side of caution, and the test should have a positive impact on returning life to normalcy.