My partner and I played a lot of games over our two month lockdown in Sydney. One of these games, Yahtzee, was somewhat new to me and I found myself becoming obsessed with trying out new strategies as we played. For those readers who are not familiar with the game of Yahtzee, you can find the basic rules here : Yahtzee Rules. I began to daydream about simulating a game of Yahtzee being played, so I could easily test out different strategies and analyse the resulting outcomes. The post below summarizes my process for building this Yahtzee simulation program, enjoy!
The Algorithm
It turns out that simulating a game of Yahtzee is no trivial matter! A game consists of 13 rounds in which a player has 3 chances to roll 1-5 die in order to maximize their score for a given category. The category the player goes for depends on what categories are left, the outcome of the first die roll, and the player’s personal strategy. The most difficult part in programming the game of Yahtzee is choosing the player’s choice for a given round.
I ended up devising a greedy algoritihm implementation, one that chooses the optimal decision based on the current situation. The algorithm decides which category the player will go for depending on the current roll of the die. This can change mid-round and it does take into account what categories have already been scored. Overall, it is not perfect, but it works.
My final program consists of three scripts and all the code can be found here : Github :
- Functions
- Play_Game
- Simulation
The Functions script include the functions for rolling the die, making the choice, and scoring for each round. I will give a brief example of the code in each function below.
The roll_dice function takes the input die_array and rolls the dice for any element that is zero. The first roll will roll all the die, and subsequent rolls of the die will depend on what choice was made from the next function.
def roll_dice(die_array):
for k in range(0,len(die_array)):
if die_array[k] == 0:
die_array[k] = rand.randint(1,6)
return die_array
The choice function is the meat of the algorithm and determines what category will be scored and changes elements in the die_array to zero in order to re-roll these again. Below, I include the logic for rolling for the Five category. There are a number of checks I perform in order to make my choice to go for the Five category. The unique_val array is simply the unique numbers rolled, and how many there were. I check to see if a number was rolled twice or more (a heuristic from experience), if 3 or 4 of a kind have already been chosen, if full house has already been chosen, if the number rolled twice or more is five, if I already have a score for 5, and finally if nothing else has been chosen yet. If all of these values are TRUE, then I decide to score the five category (at array index 4). The for loop changes any die value not equal to five to zero so it can be rolled again in order to get more fives.
#Five
if unique_val.iloc[0] >= 2 \
and x_kind_check \
and fh_check \
and unique_val.index[0] == 5 \
and score_check[4] \
and choice == 999
choice = 4
for k in range(0,len(die_array)):
if die_array[k] == 5:
die_array[k] = die_array[k]
else:
die_array[k] = 0
After I have rolled three times, it is time to calculate the final score for the round. The round_score function takes in the final choice and outputs the score. Following the Five example, the below example calculates the score by summing only the five dice. It then assigns this score to the score_array at index 4 and sets the score check array to False at index 4 to make a note that this category has been scored.
#Five score
if choice == 4:
score = 0
for k in range(0,len(die_array)):
if die_array[k] == 5 :
score = score+5
score_array[4] = score
score_check[4] = False
I won’t include the code for the play_game() function. It is fairly easy to follow and anyone interested can take a look at the code on my Github. Simply put, it loops through 13 rounds. In each round, there are three rolls of the die, and a choice is made following each roll on which die to roll again. The round score is stored, and the next round begins. At the end, the final score and which categories had a score are the output.
Simulation and Analysis
Now that my program properly plays a game of Yahtzee, I can perform simulation analysis to do some really cool things! Again, I won’t share the code here but it is available on my Github.
First, I want to run 100, 1,000, and 10,000 simulations to take a look at the resulting distributions. This will let me research the range of scores I can expect with a given strategy.
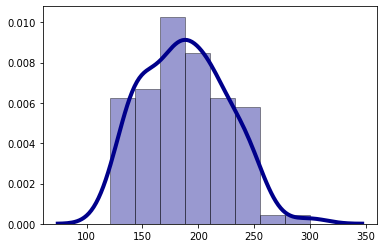
For 100 games, the resulting mean final score is 189.1 and has a standard deviation of 35.2. The distribution is below :
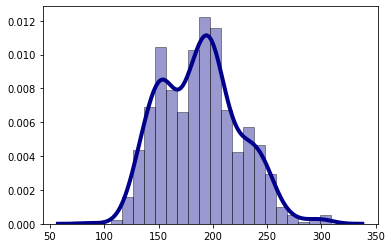
For 1,000 games, the resulting mean final score is 187.9 and has a standard deviation of 36.7. The distribution is below :
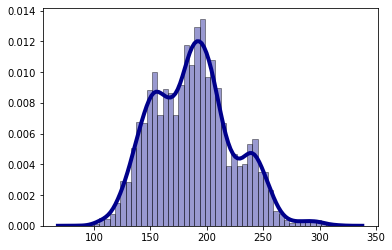
For 10,000 games, the resulting mean final score is 187.6 and has a standard deviation of 36.5. The distribution is below :
Also, the bar chart below shows the frequency of games in which the given category did not have a score :
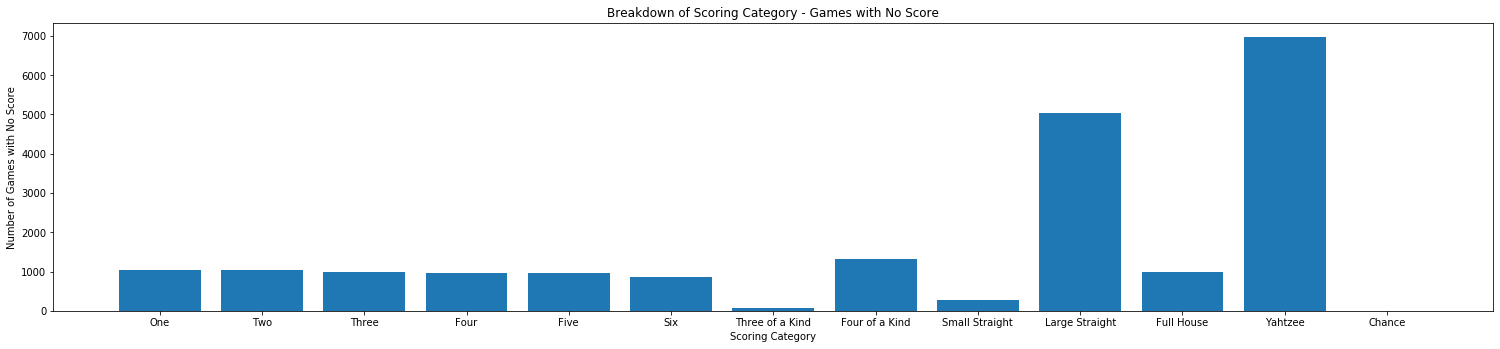
As you can see, Yahtzee and a Large Straight had the highest number of games with no score. This makes sense, as these two categories have the lowest probability of occuring.
Conclusion
This was a really neat project, and I enjoyed going through the complexities of coding the logic in Yahtzee. While my program works, it is far from the optimal solution. This paper, Optimal Yahtzee, finds an optimal value of 245 which is much higher than the mean value above of 187. My solution still has plenty of improvment in the choice logic. I look forward to continuing work on both the choice logic, and hopefully coding different strategies to simulate the resulting outcomes.